|
Software:
Linear Algebra
Functions
Ordinary Differential Equations
Systems of Nonlinear Equations
Multiple Integration
Maxima and Minima
Functions and Equations
Regression
Approximation & Interpolation
Stereographer
Math Miscellanea
Support Software
Numerical Methods:
Integration and
Differentiation
Solution of Equations
Maxima
and Minima
Approximation of Functions
Regression
Polynomial Regression
Fast
Fourier Transforms
Differential Equations
Linear Algebra Methods
Miscellaneous Procedures
Decimal
Comma/Decimal Point
| |
This collection approximates multivariable tabulated or continuous functions
in 1 to 4 independent variables
by finite multivariable power, trigonometric or mixed series.
Requirements: Windows 98
or later. |
Click on any
image for full size screenshot
Important Note:
You need programs of the Support Collection to study
these approximations. |
 |
Download Polynomial
Regression
Approximates tabulated functions in 1 to 4
independent variables by a finite multivariable power series using the Least Squares method. The program determines the
coefficients of the polynomial, the generalized correlation coefficient and the standard error of estimate. |

 |
Download Mixed Polynomial and
Trigonometric Approximations (Continuous)
Approximates continuous functions in 1 to 4 independent variables by
finite multivariable power and/or trigonometric series. The program fits the
function exactly at the grid points. |
 |
Download Mixed Polynomial and
Trigonometric Approximations (Tabulated) Approximates tabulated
functions in 1 to 4 independent variables by finite multivariable power
and/or trigonometric series. The program fits the function exactly at the
grid points. |
***You need MIXED SERIES EVALUATIONS
to study solutions obtained by the above***)
  Download
Mixed Series Evaluations Download
Mixed Series Evaluations
Evaluates
a mixed series or any partial derivative at all points of a rectangular grid
simultaneously.
|
Pending programs:
MIXED POLYNOMIAL AND TRIGONOMETRIC APPROXIMATIONS for
CONTINUOUS FUNCTIONS (FUNCTION DEFINED BY AN EQUATION) approximates IMPLICITLY defined continuous functions in 1 to 4
independent variables by finite multivariable power and/or trigonometric series. This program is similar
to the MIXED POLYNOMIAL & TRIGONOMETRIC APPROXIMATIONS for CONTINUOUS FUNCTIONS
in which functions are EXPLICITLY defined, but here the function may be defined by an equation. For instance, if the function is
y and the variable is x, then
y may be defined by the nonlinear equation
x3-4x2y+2xy2-y3=0.
FOURIER TRANSFORMS approximates tabulated functions in 1 to 4
independent variables by finite multivariable trigonometric series using fast Fourier transform methods. The program
determines the coefficients of the approximation, the generalized correlation coefficient and the standard error of estimate.
In the programs of the APPROXIMATION AND INTERPOLATION
collection, depending upon the program, the coefficients of the approximating expression are found using the method of Undetermined Coefficients, the method of Least
Squares or Fast Fourier Transform methods.
Solutions produced can be filed and such files retrieved by support programs and studied to find roots, (multiple) integral, (partial) derivatives, maxima
and minima.
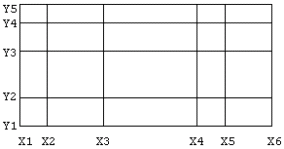
The values of tabulated functions must be taken for values of the independent variables belonging to a rectangular grid which may be unevenly
spaced, that is, a function of n variables must be tabulated at the nodes of an n-dimensional rectangular grid.
For example, if X and Y are the independent variables, we may, for instance, have 6 values of X and 5 values of Y and 30 values of the function,
one for each X-Y combination, and the grid may look like:
In the FOURIER TRANSFORMS programs, however, the grid must be evenly spaced
because fast Fourier transform methods are used. In addition, one of the versions requires the number of subintervals in any direction to be a power
of 2, while the other one only requires it to be even.
TYPES OF APPROXIMATIONS:
The programs of the APPROXIMATION AND INTERPOLATION collection produce series approximations which may be pure power, pure trigonometric or mixed power and
trigonometric series.
In all these programs, you can arrange the independent variables in any order, from innermost to outermost.
Programs which produce MIXED APPROXIMATIONS can produce not only mixed series
but also pure power series or pure trigonometric series, depending on how you
select the type of approximation in each one of the variables. In all, you may independently select, for each variable, the type of series, center of
expansion, number of terms and period (if applicable).
The POLYNOMIAL REGRESSION program will produce a pure power series. You may independently select, for each variable, the center of expansion and
number of terms.
The FOURIER TRANSFORMS programs will produce a pure trigonometric series. You may independently select, for each variable, the
number of terms.
TABULATED FUNCTIONS:
It was mentioned before that, for tabulated functions, the values of the independent variables must belong to a rectangular
grid. An example of a tabulated function with one evenly spaced variable and one
unevenly spaced is:
Y: -5
-2 2 3 6
X:
2 -720 -36 36
144 1260
3 -2880 -144 144 576
5040
4 -7200 -360 360 1440
12600
5 -14400 -720 720 2880 25200
Note that the difference between two consecutive values of X is always the same,
but the difference between two consecutive Y's varies.
An example of a tabulated function in two variables which may be approximated by the FOURIER TRANSFORMS program is:
Y: 0
p/2
p
3p/2 2p
X:
0 2 -1 2
-3 2
p/2 4 1
4 -1 4
p 2 -1
2 -3 2
3p/2 0 -3 0
-5 0
2p 2 -1
2 -3 2
Note that, even though there are 5 values in each direction, only 4 of the
function's values are independent because its value at the interval's end point must be the same as at the initial point because of the required periodicity. | |
|