Linear Algebra

Ś HOME Ś Math Software Downloads Ś Numerical Methods Ś Register Your Software Ś Contact Ś Search Ś Credit Ś

Software:
Linear Algebra
Functions
Ordinary Differential Equations
Systems of Nonlinear Equations
Multiple Integration
Maxima and Minima
Functions and Equations
Regression
Approximation & Interpolation
Stereographer
Math Miscellanea
Support Software
Numerical Methods:
Integration and Differentiation
Solution of Equations
Maxima and Minima
Approximation of Functions
Regression
Polynomial Regression
Fast Fourier Transforms
Differential Equations
Linear Algebra Methods
Miscellaneous Procedures
Decimal Comma/Decimal Point

LINEAR ALGEBRA performs computations associated with real matrices, including solution of linear systems of equations (even least squares solution of over-determined or inconsistent systems and solution by LU factors), matrix operations (add, subtract, multiply), finding the determinant, trace, inverse, adjoint, QR and LU factors, eigenvalues and eigenvectors, establish the definiteness of a symmetric matrix, perform scalar multiplication, transposition, shift, create matrices of zeroes or ones, identity, symmetric or general matrices.

Upon registering, you will receive by email a liberation key which will remove the registration reminder and the time limitation. You will be entitled to one year of free updates.

Click here to download LINEAR ALGEBRA
Requirements: Windows 98 or later

AWARDS

5 stars at onekit

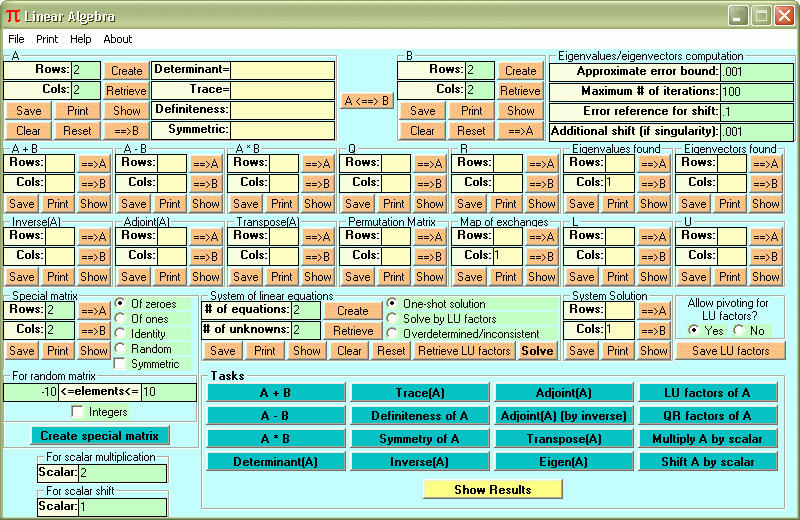
Click here to download LINEAR ALGEBRA Requirements: Windows 98 or later

LINEAR ALGEBRA performs the following tasks:

Add  Finds the sum of two matrices.

Subtract  Finds the difference of two matrices.

Multiply  Finds the product of two matrices.

Determinant  Finds the determinant of a square matrix.

Trace Finds the trace of a square matrix.

Inverse  Finds the inverse of a square matrix, if it exists.

Inverse (Compact)  Finds the inverse of a square matrix, if it exists. This version is somewhat faster and more memory efficient since it does not do the actual row exchanges for the pivoting, neither does it actually attach an identity matrix to the original one. The inverse computed is placed in the same array as the original matrix.

Adjoint  Finds the adjoint of a square matrix.

Adjoint by Inverse  Finds the adjoint of a square, nonsingular matrix.

LU Factors - Finds the LU factors of a matrix [A], that is, [L] and [U] such that [A]=[L][U], with [L] being lower-triangular and [U] being upper-triangular. In reality, the factorization can't always be done without exchanging the rows of [A] in some manner. Because of this, a permutation matrix [P] is generally involved. This makes the actual factorization [A]=[P][L][U]. Also, since the program allows [A] to be rectangular, [U] in such case would not be square so instead of upper-triangular we should more accurately call it upper-trapezoidal. This program should be used before attempting to use the program which solves simultaneous linear equations using LU factors.

QR Factors (Gram-Schmidt orthogonalization) - Factors a matrix [A] with linearly independent columns into the product [A]=[Q][R], with [Q] having orthonormal columns and [R] being upper-triangular and invertible. Since [A] must have linearly independent columns, the number of columns can't exceed the number of rows.

Test Definiteness - Establishes the positive or negative definiteness, positive or negative semidefiniteness, or indefiniteness of a symmetric matrix.

Simultaneous Linear Equations - Solves systems of linear equations using the method of Gaussian Elimination.

Simultaneous Linear Equations by LU Factors - solves systems of linear equations using the LU factorization of the matrix of coefficients. This allows quicker solution of many systems that share the same matrix of coefficients but have different right-hand sides.

Simultaneous Linear Equations - Overdetermined or Inconsistent Systems - Finds the least-squares solution to a system of linear equations which may be inconsistent or overdetermined with more equations than unknowns.

Eigenvalues and Eigenvectors - Finds the real eigenvalues and corresponding eigenvectors of a matrix. If the matrix has a full set of eigenvectors (diagonalizable), then a full set will be found even if some eigenvalues are repeated. Eigenvalues are found using the Shifted QR method. The corresponding eigenvectors are found using the Shifted Inverse Power method. Matrices are first transformed into their upper-Hessenberg form.

Transpose - Finds the transpose of a matrix.

Multiply by a Scalar  Performs scalar multiplication.

Shift  Shifts the diagonal elements of a matrix (useful in the eigenvalue problem).

Create Matrix - Creates matrices of zeroes, ones, identity matrices, symmetric, random or general matrices.