|
Software:
Linear Algebra
Functions
Ordinary Differential Equations
Systems of Nonlinear Equations
Multiple Integration
Maxima and Minima
Functions and Equations
Regression
Approximation & Interpolation
Stereographer
Math Miscellanea
Support Software
Numerical Methods:
Integration and
Differentiation
Solution of Equations
Maxima
and Minima
Approximation of Functions
Regression
Polynomial Regression
Fast
Fourier Transforms
Differential Equations
Linear Algebra Methods
Miscellaneous Procedures
Decimal
Comma/Decimal Point
| |
|
This collection
produces
stereographs of mathematical functions, mixed series and regression results. When properly viewed,
they provide a true 3D effect.
Requirements: Windows 98
or later. |
Click on any
image for full size screenshot
To view each stereograph,
cross your eyes and
merge the two images |



 |
Download Stereographer
Produces
stereographs of mathematical functions or of approximations to the 1st and
2nd order partial derivatives of a function of 2 variables.
|
The
above
are STEREOSCOPIC GRAPHS which give the
realistic sensation of depth like those 3D viewers we all had as children. But
these are designed for free viewing and are cross-eyed
stereographs, so the image corresponding to the right eye is on the
left and vice-versa. See instructions below.
Surfaces or space curves
can be stereographed.
The
representation can be
nonparametric: z = f(x,y)
or parametric:
x = x(u,v) ; y = y(u,v)
; z = z(u,v) (where u and v are the parameters)
You can visualize, for instance,
the hyperbolic
paraboloid
z
=
(x2/25-y2/16)/6
or the sphere
x = 2*sin(u)*cos(v) ; y =
2*sin(u)*sin(v) ; z = 2*cos(u)
Pending programs:
STEREOGRAPHER - FOR MIXED SERIES IN 2
VARIABLES stereographs any 2-variable polynomial, trigonometric, or mixed series of the type produced by programs of
the APPROXIMATION AND INTERPOLATION collection or by the MIXED SERIES CREATION
program of the SUPPORT collection. Also, any partial derivative of the series
can be stereographed. In addition, the original points used to find the series
can also be stereographed. These are either the original grid points used to
approximate a continuous function, or the original tabulated function.
STEREOGRAPHER - FOR REGRESSION ANALYSIS RESULTS stereographs any 2-variable
regression surface produced by the programs of the REGRESSION collection (such a
file must first be converted by the program which converts files from results of
REGRESSION to STEREOGRAPHER, which is in the same diskette). In addition, the
original points used to find the regression surface can also be stereographed.
Authentic depth perception requires that each eye receive a slightly different
view of an object, that is, from two slightly different angles. The pair of
side-by-side graphs in a stereograph look very similar, but they are not
identical. Each represents a view of an object from slightly different angles.
If you feed one view to one eye and the other view to the other eye, the brain
blends this information to give you the sensation of three-dimensionality.
Stereographs produced by this collection can be viewed by most without the aid
of a stereoscope. This is because almost everyone can cross their eyes at will
since this is precisely what they do when they focus on an object which is only
a few inches from their eyes. In these stereographs the view for the right eye
is placed on the left, and vice versa, as illustrated in the figure below. The
area labeled R holds the view for the RIGHT eye and the area labeled L holds the
view for the LEFT eye. We thus loosely call them "cross-eyed"
stereographs.
You can practice with a stereograph displayed on the screen or with a printout
of a stereograph laid flatly on a surface. Aim your sight perpendicularly at the
center of the line which separates the two views. Start crossing your eyes until
the two images merge.
The following is a simple cross-eyed stereograph. If you can merge the two words
you will feel a depth sensation.
If you are one of the people that have some difficulty controlling your eyes in
the required manner, practice by first viewing the stereographs from a few feet
away and move in closer until you are at a normal distance from the screen. In
addition, you can develop smaller stereographs using a reduction factor of less
than 1, for instance .5 or even .25. With a reduced stereograph, since the two
views are closer together, a lesser degree of eye-crossing is needed to view
them. You can slowly increase the reduction factor until you are capable of
viewing a full size stereograph.
You can use a pencil to exercise the required muscles. Hold it at arm's length,
focus your eyes on it, then slowly bring it as close to your nose as possible
without loosing the focus. It may help if your head is tilted back somewhat. In
fact, if you have a stereograph in the background, it is possible that you would
notice the two images merging as the pencil gets closer to your nose. Once you
learn to merge the two images, it is easy to keep a lock on them because the
brain is accustomed to receiving different information from the two eyes and
combining them to give the true three-dimensional sensation we get from real
solid objects.
The only skill required is that you be able to cross your eyes. Remember,
everyone can do it. In fact, most of the time our eyes are slightly crossed
because the objects we look at are not at infinity. If you need some practice,
it will be worth it. Stereographs provide a fascinating sensation.
You have full control on the characteristics of the graph since you will place
the axes wherever you wish, determine the size of the divisions to be placed on
them, set the X and Y ranges (or U and V ranges for the parametric version), set
the number of grid lines by setting the number of spacings, select the number of
plotting segments per spacing, define the X, Y and Z windows. If you wish to
translate and/or rotate the figure, you enter the desired X, Y and Z
translations and the rotations about the X, Y and Z axes. If you wish to have
the surface represented by dots randomly scattered on it, you select the number
of dots you wish generated. You can use grid lines alone, dots alone, or both.
You even control the stereoscopic factor, thereby adjusting the magnitude of the
three-dimensional effect to suit your perceptions. In addition, reduced size
stereographs can be developed if so desired. In the case of the MIXED SERIES and
the REGRESSION versions, you can also have plotted the original data thereby
visualizing the three-dimensional scatter diagram.
Once you have set up a nice stereograph, you can store all the details in a disk
file which you can retrieve at will.
Check
out some stereographs produced by the
old
GWBasic Stereographer!
|
To
view each stereograph,
cross your eyes
and merge the two images |
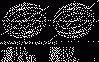



|
|
Click on
any image for full size stereograph
|
 |
Click and be patient with this one
if you have a slow connection. It's
an animated gif - 248KB. When fully loaded it'll show a rotating torus. |
|
AWARDS |
|
|
 |
|
| |
|